(Probably, this is a standard algorithm, so if someone knows the name, drop me a note.)

If something like

$y_i = {x_i a \over b}$

is to be calculated, and all numbers are integers, a naive implementation would result in something, for which

$\sum y_i \ne {(\sum x_i) a \over b}$

because of rounding errors, due to the integer division. This can be avoided by transforming the formula into

$y_i = {(\sum_{j=0}^{j=i} x_j) a \over b} - \sum_{j=0}^{j=i-1} y_j$

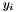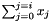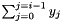Of corse, when all $y_i$ are calculated in a sequence, $\sum_{j=0}^{j=i} x_j$ and $\sum_{j=0}^{j=i-1} y_j$ can be accumulated in the same loop. Regard this as sample:

int n, x[n], a, b; // Should all be initialized.
int y[n], cumX = 0, cumY = 0;
for (int i = 0; i < n; i++) {
   cumX += x[i]
   y[i] = (cumX * a) / b - cumY;
   cumY += y[i];
}