Dillo v3.1.1-99-gf3103cc4
Loading...
Searching...
No Matches
Changes in Line-Breaking and Hyphenation
Info: Should be incorporated into dw::Textblock.

Introduction

For the implementation of hyphenation in dillo, not only a hyphenation algorithm was implemented, but also, the line breaking was changed to a simple optimization per line. Aside from the improvement by this change per se, an important aspect is the introduction of "penalties". Before this change, dillo put all words into a line which fitted into it; now, a "badness" is calculated for a possible breakpoint, and the best breakpoint, i. e. the breakpoint with the smallest value for "badness", is chosen. This can be simply refined to define "good" and "bad" breakpoints by assigning a "penalty"; the best breakpoint is then the one with the smallest value of "badness + penalty". Details can be found below.

Example: Normal spaces have a penalty of 0, while hyphenation points get a penalty of, say, 1, since hyphenation is generally considered as a bit "ugly" and should rather be avoided. Consider a situation where the word "dillo" could be hyphenated, with the following badnesses:

  • before "dillo": 0.6;
  • between "dil-" and "lo": 0.2;
  • after "dillo": 0.5.

Since the penalty is added, the last value is the best one, so "dillo" is put at the end of the line, without hyphenation.

Under other circumstances (e. g. narrower lines), the values might be different:

  • before "dillo": infinite;
  • between "dil-" and "lo": 0.3;
  • after "dillo": 1.5.

In this case, even the addition of the penalty makes hyphenation the best choice.

Literature

Breaking Paragraphs Into Lines

Although dillo does not (yet?) implement the algorithm TEX uses for line breaking, this document shares much of the notation used by the article Breaking Paragraphs Into Lines by Donald E. Knuth and Michael F. Plass; originally published in: Software – Practice and Experience 11 (1981), 1119-1184; reprinted in: Digital Typography by Donalt E. Knuth, CSLI Publications 1999. Anyway an interesting reading.

Hyphenation

Dillo uses the algorithm by Frank Liang, which is described in his doctoral dissertation found at http://www.tug.org/docs/liang/. There is also a description in chapter H ("Hyphenation") of *The TEXbook* by Donald E. Knuth, Addison-Wesley 1984.

Pattern files can be found at http://www.ctan.org/tex-archive/language/hyphenation.

Overview of Changes

Starting with this change, dw/textblock.cc has been split up; anything related to line breaking has been moved into dw/textblock_linebreaking.cc. This will also be done for other aspects like floats. (Better, however, would be a clean logical split.)

An important change relates to the way that lines are added: before, dillo would add a line as soon as a new word for this line was added. Now, a line is added not before the last word of this line is known. This has two important implications:

  • Some values in dw::Textblock::Line, which represented values accumulated within the line, could be removed, since now, these values can be calculated simply in a loop.
  • On the other hand, this means that some words may not belong to any line. For this reason, in some cases (e. g. in dw::Textblock::sizeRequestImpl) dw::Textblock::showMissingLines is called, which creates temporary lines, which must, under other circumstances, be removed again by dw::Textblock::removeTemporaryLines, since they have been created based on limited information, and so possibly in a wrong way. (See below for details.)

When a word can be hyphenated, an instance of dw::Textblock::Word is used for each part. Notice that soft hyphens are evaluated immediately, but automatic hyphenation is done in a lazy way (details below), so the number of instances may change. There are some new attributes: only when dw::Textblock::Word::canBeHyphenated is set to true*, automatic hyphenation is allowed; it is set to false when soft hyphens are used for a word, and (of course) by the automatic hyphenation itself. Furthermore, dw::Textblock::Word::hyphenWidth (more details in the comment there) has to be included when calculating line widths.

Some values should be configurable: dw::Textblock::HYPHEN_BREAK, the penalty for hyphens. Also dw::Textblock::Word::stretchability, dw::Textblock::Word::shrinkability, which are both set in dw::Textblock::addSpace.

Criteria for Line-Breaking

Before these changes to line breaking, a word (represented by dw::Textblock::Word) had the following attributes related to line-breaking:

In a more mathematical notation, the $i$th word has a width $w_i$ and a space $s_i$.

A break was possible, when there was a space between the two words, and the first possible break was chosen.

With hyphenation, the criteria are refined. Hyphenation should only be used when otherwise line breaking results in very large spaces. We define:

  • the badness $\beta$ of a line, which is greater the more the spaces between the words differ from the ideal space;
  • a penalty 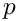$p$ for any possible break point.

The goal is to find those break points, where $\beta + p$ is minimal.

Examples for the penalty $p$:

  • 0 for normal line breaks (between words);
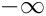  • $\infty$ to prevent a line break at all costs;
  • $-\infty$ to force a line
  • a positive, but finite, value for hyphenation points.

So we need the following values:

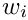  • $w_i$ (the width of the word 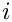$i$ itself);
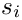  • $s_i$ (the width of the space following the word $i$);
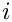  • the stretchability 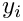$y_i$, a value denoting how much the space after word 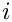$i$ can be stretched (typically 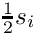${1\over 2} s_i$ for justified text; otherwise 0, since the spaces are not stretched);
  • the shrinkability 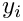$y_i$, a value denoting how much the space after word 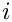$i$ can be shrunken (typically 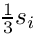${1\over 3} s_i$ for justified text; otherwise 0, since the spaces are not shrinked);
  • the penalty 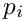$p_i$, if the line is broken after word $i$;

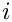  • a width 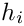$h_i$, which is added, when the line is broken after word $i$.

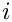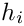    $h_i$ is the width of the hyphen, if the word 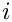$i$ is a part of the hyphenated word (except the last part); otherwise 0.

Let $l$ be the (ideal) width (length) of the line, which is e. at the top given by the browser window width. Furthermore, all words from $a$ to $b$ are added to the line. $a$ is fixed: we do not modify the previous lines anymore; but our task is to find a suitable $b$.

We define:

\[W_a^b = \sum_{i=a}^{b} w_i + \sum_{i=a}^{b-1} s_i + h_b\]

\[Y_a^b = {Y_0}_a^b + \sum_{i=a}^{b-1} y_i\]

\[Z_a^b = {Z_0}_a^b + \sum_{i=a}^{b-1} z_i\]

$W_a^b$ is the total width, $Y_a^b$ the total stretchability, and $Z_a^b$ the total shrinkability. ${Y_0}_a^b$ and ${Z_0}_a^b$ are the stretchability and shrinkability defined per line, and applied at the borders; they are 0 for justified text, but ${Y_0}_a^b$ has a positive value otherwise, see below for details.

Furthermore the adjustment ratio $r_a^b$:

  • in the ideal case that $W_a^b = l$: $r_a^b = 0$;
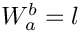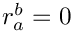  • if 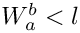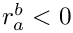$W_a^b < l$: $r_a^b = (l - W_a^b) / Y_a^b$ ( $r_a^b < 0$ in this case);
  • if 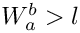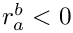$W_a^b > l$: $r_a^b = (l - W_a^b) / Z_a^b$ ( $r_a^b < 0$ in this case).

The badness $\beta_a^b$ is defined as follows:

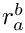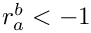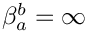  • if $r_a^b$ is undefined or $r_a^b < -1$: $\beta_a^b = \infty$;
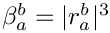
  • otherwise: $\beta_a^b = |r_a^b|^3$

The goal is to find the value of $b$ where $\beta_a^b + p_b$ is minimal. ( $a$ is given, since we do not modify the previous lines.)

After a couple of words, it is not predictable whether this minimum has already been reached. There are two cases where this is possible for a given $b'$:

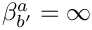  • $\beta_{b'}^a = \infty$ (line gets too tight): 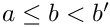$a \le b < b'$, the minimum has to be searched between these two values;
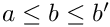  • $p_{b'} = -\infty$ (forced line break): $a \le b \le b'$ (there may be another minimum of 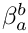$\beta_a^b$ before; note the $\le$ instead of $<$).

This leads to a problem that the last words of a text block are not displayed this way, since they do not fulfill these rules for being added to a line. For this reason, there are "temporary" lines already described above.

(Note that the actual calculation differs from this description, since integer arithmetic is used for performance, which make the actual code more complicated. See dw::Textblock::BadnessAndPenalty for details.)

Ragged Borders

For other than justified text (left-, right-aligned and centered), the spaces between the words are not shrinked or stretched (so $y_i$ and $z_i$ are 0), but additional space is added to the left or right border or to both. For this reason, an additional stretchability ${Y_0}_a^b$ is added (see definition above). Since this space at the border is 0 in an ideal case ( $W_a^b = l$), it cannot be shrunken, so ${Z_0}_a^b$ is 0.

This is not equivalent to the calculation of the total stretchability as done for justified text, since in this case, the stretchability depends on the number of words: consider the typical case that all spaces and stretchabilities are equal ( $y_a = y_{a + 1} = \ldots = y_b$). With $n$ words, the total strechability would be $n \cdot y_a$, so increase with an increasing number of words ( $y_a$ is constant). This is correct for justified text, but for other alignments, where only one space (or two, for centered text) is changed, this would mean that a line with many narrow words is more stretchable than a line with few wide words.

It is obvious that left-aligned text can be handled in the same way as right-aligned text. [... Centered text? ...]

The default value for the stretchability is the line height without the space between the lines (more precisely: the maximum of all word heights). The exact value not so important when comparing different possible values for the badness $\beta_a^b$, when ${Y_0}_a^b$ is nearly constant for different $b$ (which is the case for the actual value), but it is important for the comparison with penalties, which are constant. To be considered is also that for non-justified text, hyphenation is differently (less) desirable; this effect can be achieved by enlarging the stretchability, which will lead to a smaller badness, and so make hyphenation less likely. The user can configure the stretchability by changing the preference value stretchability_factor* (default: 1.0).

(Comparison to TEX: Knuth and Plass describe a method for ragged borders, which is effectively the same as described here (Knuth 1999, pp. 93–94). The value for the stretchability of the line is slightly less, 1 em (ibid., see also p. 72 for the definition of the units). However, this article suggests a value for the hyphenation penalty, which is ten times larger than the value for justified text; this would suggest a larger value for stretchability_factor*.)

Hyphens

Words (instances of dw::Textblock::Word), which are actually part of a hyphenated word, are always drawn as a whole, not seperately. This way, the underlying platform is able to apply kerning, ligatures, etc.

Calculating the width of such words causes some problems, since it is not required that the width of text "AB" is identical to the width of "A" plus the width of "B", just for the reasons mentioned above. It gets even a bit more complicated, since it is required that a word part (instance of dw::Textblock::Word) has always the same length, independent of whether hyphenation is applied or not. Furthermore, the hyphen length is fixed for a word; for practical reasons, it is always the width of a hyphen, in the given font.

For calculating the widths, consider a word of four syllables: A-B-C-D. There are 3 hyphenation points, and so 23 = 8 possible ways of hyphenation: ABCD, ABC-D, AB-CD, AB-C-D, A-BCD, A-BC-D, A-B-CD, A-B-C-D. (Some of them, like the last one, are only probable for very narrow lines.)

Let w(A), w(B), w(C), w(D) be the word widths (part of dw::Textblock::Word::size), which have to be calculated, and l be a shorthand for dw::core::Platform::textWidth. Without considering this problem, the calculation would be simple: w(A) = l(A) etc. However, it gets a bit more complicated. Since all non-hyphenations are drawn as a whole, the following conditions can be concluded:

  • from drawing "ABCD" (not hyphenated at all): w(A) + w(B) + w(C) + w(D) = l(ABCD);
  • from drawing "BCD", when hyphenated as "A-BCD" ("A-" is not considered here): w(B) + w(C) + w(D) = l(BCD);
  • likewise, from drawing "CD" (cases "AB-CD" and "A-B-CD"): w(C) + w(D) = l(CD);
  • finally, for the cases "ABC-D", "AB-C-D", "A-BC-D", and "A-B-C-D": w(D) = l(D).

So, the calculation is simple:

  • w(D) = l(D)
  • w(C) = l(CD) - w(D)
  • w(B) = l(BCD) - (w(C) + w(D))
  • w(A) = l(ABCD) - (w(B) + w(C) + w(D))

For calculation the hyphen widths, the exact conditions would be over-determined, even when the possibility for individual hyphen widths (instead of simply the text width of a hyphen character) would be used. However, a simple approach of fixed hyphen widths will have near-perfect results, so this is kept simple.

Automatic Hyphenation

When soft hyphens are used, words are immediately divided into different parts, and so different instances of dw::Textblock::Word. Automatic hyphenation (using Liang's algorithm) is, however, not applied always, but only when possibly needed, after calculating a line without hyphenation:

  • When the line is tight, the last word of the line is hyphenated; possibly this will result in a line with less parts of this word, and so a less tight line.
  • When the line is loose, and there is another word (for the next line) available, this word is hyphenated; possibly, some parts of this word are taken into this line, making it less loose.

After this, the line is re-calculated.

A problem arrises when the textblock is rewrapped, e. g. when the user changes the window width. In this case, some new instances of dw::Textblock::Word must be inserted into the word list, dw::Textblock::words. This word list is implemented as an array, which is dynamically increased; a simple approach would involve moving all of the n elements after position i, so n - i steps are necessary. This would not be a problem, since O(n) steps are necessary; however, this will be necessary again for the next hyphenated word (at the end of a following line), and so on, so that (n - i1) + (n - i2) + ..., with i1 < i2 < ..., which results in O(n2) steps. For this reason, the word list is managed by the class lout::misc::NotSoSimpleVector, which uses a trick (a second array) to deal with exactly this problem. See there for more details.

Tests

There are test HTML files in the test directory. Also, there is a program testing automatic hyphenation, test/liang, which can be easily extended.

Bugs and Things Needing Improvement

High Priority

None.

Medium Priority

None.

Low Priority

Mark the end of a paragraph:** Should dw::core::Content::BREAK still be used? Currently, this is redundant to dw::Textblock::BadnessAndPenalty.

Solved (Must Be Documented)

These have been solved recently and should be documented above.

Bugs in hyphenation:* There seem to be problems when breaking words containing hyphens already. Example: "Abtei-Stadt", which is divided into "Abtei-" and "Stadt", resulting possibly in "Abtei--[new line]Stadt". See also below under "Medium Priority", on how to deal with hyphens and dashes.

Solution:** See next.

Break hyphens and dashes:* The following rules seem to be relevant:

  • In English, an em-dash is used with no spaces around. Breaking before and after the dash should be possible, perhaps with a penalty > 0. (In German, an en-dash (Halbgeviert) with spaces around is used instead.)
  • After a hyphen, which is part of a compound word, a break should be possible. As described above ("Abtei-Stadt"), this collides with hyphenation.

Where to implement? In the same dynamic, lazy way like hyphenation? As part of hyphenation?

Notice that Liang's algorithm may behave different regarding hyphens: "Abtei-Stadt" is (using the patterns from CTAN) divided into "Abtei-" and "Stadt", but "Nordrhein-Westfalen" is divided into "Nord", "rhein-West", "fa", "len": the part containing the hyphen ("rhein-West") is untouched. (Sorry for the German words; if you have got English examples, send them me.)

Solution for both:** This has been implemented in dw::Textblock::addText, in a similar way to soft hyphens. Liang's algorithm now only operates on the parts: "Abtei" and "Stadt"; "Nordrhein" and "Westfalen".

Hyphens in adjacent lines:* It should be simple to assign a larger penalty for hyphens, when the line before is already hyphenated. This way, hyphens in adjacent lines are penalized further.

Solved:** There are always two penalties. Must be documented in detail.

Incorrect calculation of extremes:* The minimal width of a text block (as part of the width extremes, which are mainly used for tables) is defined by everything between two possible breaks. A possible break may also be a hyphenation point; however, hyphenation points are calculated in a lazy way, when the lines are broken, and not when extremes are calculated. So, it is a matter of chance whether the calculation of the minimal width will take the two parts "dil-" and "lo" into account (when "dillo" has already been hyphenated), or only one part, "dillo" (when "dillo" has not yet been hyphenated), resulting possibly in a different value for the minimal width.

Possible strategies to deal with this problem:

  • Ignore. The implications should be minimal.
  • Any solution will make it neccessary to hyphenate at least some words when calculating extremes. Since the minimal widths of all words are used to calculate the minimal width of the text block, the simplest approach will hyphenate all words. This would, of course, eliminate the performance gains of the current lazy approach.

  • The latter approach could be optimized in some ways. Examples: (i) If a word is already narrower than the current accumulated value for the minimal width, it makes no sense to hyphenate it. (ii) In other cases, heuristics may be used to estimate the number of syllables, the width of the widest of them etc.

    Solved:** Hyphenated parts of a word are not considered anymore for width extremes, but only whole words. This is also one reason for the introduction of the paragraphs list.

    Also:**

  • Configuration of penalties.